剑指 Offer 68 - II. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

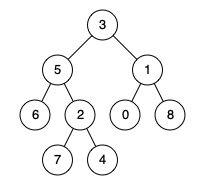
示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

Solution 1

中序遍历，用栈记录访问过的节点
在未访问到p和q之前，栈为root到当前节点的路径。
当访问到p和q之一之后，最近公共祖一定在栈内，此时栈不入只出。
当p和q都被访问到之后，栈顶元素为最近公共祖，停止遍历，拒绝修改栈。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
import java.util.*;

class Solution {
    boolean foundOne;
    boolean foundTwo;
    Stack<TreeNode> stack;

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        foundOne = foundTwo = false;
        stack = new Stack<>();
        inorderTraversal(root, p, q);
        return stack.peek();
    }

    private void inorderTraversal(TreeNode node, TreeNode p, TreeNode q) {
        if (node == null || foundTwo)
            return;
        boolean pushed = false;
        if (!foundOne) {
            stack.push(node);
            pushed = true;
        }
        if (foundOne == true && (node == p || node == q))
            foundTwo = true;
        if (foundOne == false && (node == p || node == q))
            foundOne = true;
        inorderTraversal(node.left, p, q);
        inorderTraversal(node.right, p, q);
        if (pushed && !foundTwo)
            stack.pop();
    }
}

Solution 2

后续遍历，利用返回值判断
如果n是最近公共祖先，n就是p和q的第一个公共父节点(这里父节点额外包括本身)
那么p和q必定分别出现在n左右子树，或者是p或q就是n，之后只需要找父节点的交集
用返回值作为标识，不为null代表返回的节点是p或q的父节点，其左右子树中出现了p或q
如果node的左右子树中分别出现p和q，说明node就是最近公共祖先，返回node本身。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return postorderTraversal(root, p, q);
    }

    private TreeNode postorderTraversal(TreeNode node, TreeNode p, TreeNode q) {
        if (node == null)
            return null;
        TreeNode left = postorderTraversal(node.left, p, q);
        TreeNode right = postorderTraversal(node.right, p, q);
        if (node == p || node == q)
            return node;
        if (left == null && right == null)
            return null;
        else if (left == null)
            return right;
        else if (right == null)
            return left;
        else // if (left != null && right != null)
            return node;
    }
}